Introduction One of the obstacles for a student to tackle any problem is the lack of ability to grasp the whole picture of the scenario that the question is asking and the second obstacle is the ability to decide the steps to solve it or break down into simpler chunks. Problems can be routine or non-routine ones. Routine ones can be easily solved by memorizing the rules and formulas. Non-routine ones require special strategies. One of the strategies is to use “heuristic”. The word “heuristic” came from the Greek verb, heuriskein which means “to discover”. There are many ways to go about to solving a complex problem sum. The ways and methods are also known as heuristics. There are 4 basic steps that a student can take to solve a problem: Step one: Comprehend the problem. A student has to understand the problem or to be able to visualize the scenario first. If the problem sum is very wordy, the student should focus on the key components. Some of the words are used to cause confusion and does not play any role for the answer. Next, the student should break the question into smaller portion so as to ease digestion in their mind. A student might need to draw models or diagram so as to help him to visualize the scenario of the question given. If the students fail to visualize the problem correctly, they will not be able to choose the correct means to solve the problem. Step Two: Decide on an strategies or approach There are many methods or approaches to solve a problem and the student need to decide one which best suit the requirements. Step 3: Action to solve the problem After deciding on the strategy to be implemented, the next stage is to implement the strategy selected for the problem. At this stage, the student may discover that they might need another strategy to work together in order to solve the problem or realized that they have implemented a wrong strategy. In such a case, the student need to go back to step two, which is to analyse which strategies to use. Step 4: Checking the solution After the problem has been solved, it is important to validate the answer to ensure that the answer is rational and reasonable. One method is “working backwards”. If the student is able to get the original value, most likely the answer is correct. A student who is trained with the “heuristic” mindset can: Use the problem-solving approach to identify and comprehend the problem content. Use the approach to resolve problems in everyday life. Be pro-active and creative in problem solving. Be confident in tackling any complex mathematical problem. Apply mathematics solution in meaningful ways in various situations. Visualisation One of the main components of “heuristic” methods is to visualize. In fact, we use visualisation to solve simple and complex problems in our daily live, which require spatial imagination or the ability to make assumption or prediction based on the presented and remembered facts. Visualisation is a powerful method, which can be applied to mathematics to increase students’ ability to solve math problems. Before coming to any conclusion on how to solve the problem, it is essential to understand the questions and how the mathematical concepts and tools can come in to fix the problem. There is a proverb that says “a picture is worth a thousand word”. One method to help students to visualize a problem is to draw a diagram. Visualisation however is not limited to drawing visual representations of the objects, but it can be used at every step of solving math problems. So why is visualisation is applied in the first place? Firstly, it is applied to understand and define the scope of the problem. Without visualisation, it is impossible to estimate the scale and its mathematical relationship. A lot of students who failed at solving complex math problems is because they failed to visualise the problem and thus they are not able to choose the right means to solve the problem or take a long time to realise what the question is asking for. Secondly, for advance math like modeling (e.g. 3D or 2 dimensional geometry question), it is very difficult for anyone to solve such calculations without mastering the visualisation skill in the early stage. Finally, it is a tool for estimation and projection (predicting). This skill is crucial for solving complex math problems which require multiple operations on the equations performed in a correct order. Students who are able to visualise can predict the outcome if they are to apply certain rules of math. Student who are trained in visualising problems in their early stage will tend to solve problems accurately if not faster than those who purely memorising the formulae (though most of the time they can solve problems at a faster speed). That is because when the problem is being modified or altered, being different from the norm, students who mastered visualisation will be able to detect the difference and are versatile in tackling the problem whereas students who depend on memorizing the steps will have difficulties understanding the problem even though the solution is almost similar. Using Model Approach One of the most common visualisation method is using model. You do not need to be a great artist to use the model approach to solve mathematical problems. It uses simple shapes (e.g., rectangles) to represent an object. The models are used to illustrate the relationships that exist between different entities (persons, objects or events) in a given scenario in the problem. In the lower primary school level, students should have been introduced to some basic model-drawing method or commonly known as the bar method. When teaching addition and subtraction, two commonly used models are the Part-whole and Comparison model. The Model approach is one of the best ways to teach lower primary students to understand the mathematical relationship between various entities. Many students typically find some word problems very challenging. This could be due to their lack of mathematical language understanding or limited arithmetic operations. Many students also struggle to relate the knowns to the unknowns when the problem is modified in different structures hence hindering them to analyze problem situation. When such cases arise, students tend to lose confidence in solving math problems. This will be brought forth even to their adulthood. However without much practice and guidance, students or parents will find it difficult to experience the full benefits of the model method. The model method is a good start to help children in the early stage to identify the key components and breaks them into smaller discrete portions hence solving it systematically. Modelling is to draw rectangular boxes to represent part-whole relationships and math values (Known and unknown values). Students who use the modelling approach is able to map the concept to the real-life situations. By illustrating using boxes or blocks, it provides a great visualisation tool for students to explain the logic clearly and thus able to make tacit knowledge explicit. Using Modelling approach is one of the most recommended technique in Singapore. The usage of models goes beyond solving simple addition and subtraction, it is used often in more complex topic like fractions, ratios or percentages. All these high level topics could be a great challenge for some young children but with the usage of modelling, it illustrates the relationships between various entities and therefore provides a clearer image in their mind to tackle the problem. A good modelling skill provides a clear mapping tool to the complex interrelated components in the math problem sum. Looking for a pattern This approach can be applied when there is pattern detected when a set of data is collected. This method is suitable for questions related to statistics as most of the data tend to have some similar occurrence. By observing each given set of element or information, one at a time in consecutive sequence, it is able to detect what the next elements will be in the next sequence. In fact, in our daily life, we can see patterns are all around us. Finding the patterns allow us to predict the future, discover new things and better understand the surrounding around us. The objective of observing a pattern is to predict the next outcome. What will the 55th number of this pattern be? How many cheese cakes need to be ordered if the party is meant for a school instead of just a class? Working with number patterns leads directly to the concept of functions in Mathematics: a formal description of the relationships among different quantities. If you can find a pattern, you can use that pattern to generalise what you see into a broader solution to a problem. At the early stage, they can learn patterns by counting by 1s, then by 2s and so on. These patterns provide them a natural strategy to understand addition and multiplication. Now considering a number pattern such as 3, 6, 9…, a student will ask himself, which number can I add to get the next number in the pattern and the next and the next and so on? As they advance, their knowledge of patterns advances them from simple addition/subtraction to multiplication/division. At higher stages, they can understand functions, such as f(x) = 2x + 2, where x is the numerical sequence of 0,1,2,3….. They begin with simple in-out machines which gradually provide a great foundation to complex algebra work. Guess and Check This is one of the most powerful strategies in the process of solving mathematical problems. Students are to make guesses and then refine their guesses during the process until a correct answer has been devised. This approach develops their logical reasoning. The strategy allows the student to fine-tune their “answer” and require some perseverance for trial and error refinement until a perfect solution is devised. To apply this strategy, you need to have complete understanding of the requirement first. Identify the conditions given in the problem which have to be fulfilled. When making a guess, the answer being guessed will be checked if it fulfilled all the conditions. If the conditions are fulfilled, then it is the correct answer (or could be one of the correct answer). If any of the conditions is not satisfied, then it is not the answer. Such an approach is the most time consuming. In real life, there may not be an exact formulae to get the answer immediately hence trial and error is needed to solve it. All research mathematicians will need to use the guess and check method, and it is one of the most powerful methods of solving differential equations, which are equations involving an unknown function and its’ derivatives. The main difference between problem solving in the academic background and in real life situation is that, for the well tested problem, the solution is already known but in the real scientific or research environment, the solution is unknown, so checking is required to validate. This is a flexible method and it is often taught in school as a starting point. It is used as a safety net when students do not know what other methods can be used. Since this is the easiest to implement, many student stick on this method and forsake other more effective methods. Guess and check is the most time consuming strategy and it is best used to check the answer rather than solving the problem unless there is no other methods to be used. Make a list This involves making an organised list by using the data given. This strategy allows students to clearly examine the data and draw a conclusion from it. It is easier to examine a list of organised data than looking at the unstructured data. They can discover the pattern in the data and use them to solve the problems. Finding and understanding patterns is important factors that contribute to mathematical problem solving. It is easier for students to understand the patterns if they know how to structure or organise the data. Once the data is organised, it can be processed at much ease and turn out to be a valuable database for translating meaningful information. Many students find it helpful if the data is well organised. This process requires or enables them to think more deeply about each piece of data given and to think about how those pieces fit together. Organised data will enable students to see patterns and learn mathematical concepts more easily. It will also help them to think about what do and what they do not know about a problem. Organised list are fairly easy to create as long as there are not a lot of items. In our working environment, we do create lists of data using excel sheet and then process it into a chart for more meaningful presentation. Work Backwards This is also known as bottom-up method. It is using reverse operation to find the data at the beginning of the situation. Take for example: Question: Jack walked from Queenstown to Jurong West. He took 1 hour 30 minutes to walk from Queenstown to Jurong East. Then he took 25 minutes to walk from Jurong East to Jurong West. He arrived at Jurong West at 2:45 P.M. At what time did he leave Queenstown? Strategy: UNDERSTAND: What do you need to find? You need to find what the time was when Jack left Queenstown. PLAN: How can you solve the problem? You can work backwards from the time Jack reached Jurong West. Subtract the time it took to walk from Jurong East to Jurong West. Then subtract the time it took to walk from Queenstown to Jurong East. SOLVE: Start at 2:45pm. This is the time Jack reached Jurong West. 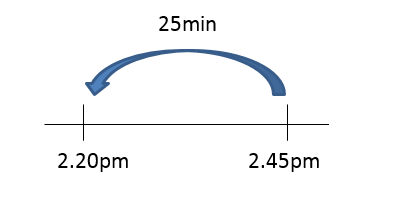Work backwards by 25 minutes. This is the time it took to get from Jurong East to Jurong West. Time is: 2.20 P.M. 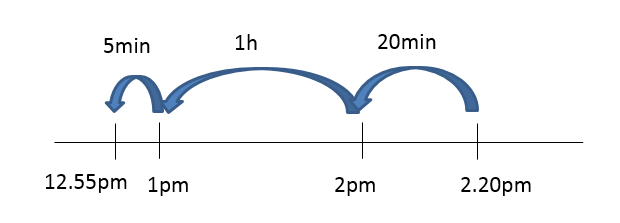Work backwards by 1 hour 25 minutes. This is the time it took to get from Queenstown to Jurong East. Jack left Queenstown at 12:55 P.M. The question is asking about the past and not the future or present. Thus, a work backwards method can be used for this scenario. When students use this method to solve the problem, encourage them to show the workings and to present it clearly so that they can keep track of what they are processing. Estimation In typical mathematics problem, we often emphasised on getting an exact answer to the question. But in everyday life, we do not focus on the exact but rather on estimation. One example is on money spend. Usually we look at the the dollars rather than the cents. One of the benefits of estimation is to save time when the calculation does not require to be exact. It also helps to check the correct answer faster if time is not at your side. Estimation is a higher-level skill that requires students to be able to conceptualise and mentally manipulate numbers. Estimating is an important skill. It allows students to be able to determine the reasonableness of their answer. Without estimation skills, students will not able to determine if their answer is within an acceptable range. This inability causes them to make computational errors within it even being on their range. Estimations allow rapid calculations without the need of using calculator. At their early stage, they are encouraged to develop the strategy of “eyeballing” a small group and using this benchmark to estimate how many are in a larger group. There are many ways to make estimation including rounding off, finding compatible numbers, bracketing and compensating. Open-ended Open-ended problems cater to wider range of mathematical abilities and stage of development in student. Creating an open-ended question is tricky and requires students to go beyond their traditional thinking and not be afraid to make mistakes. In open-ended questions, there could be multiple solutions that cater for a wide range of mathematical abilities and stages of development in children. Students participate more actively in lessons and express their ideas more frequently. The Open-Ended Problem Solving provides free, responsive, and supportive learning environment because there are many different correct solutions, so that each student has opportunities to get own unique answer(s). Therefore, students are curious about other solutions, and they can compare with and discuss their solutions with each other. As students are very active, it brings a lot of interesting conversation to the classroom. Students have more opportunities to make comprehensive use of their mathematical knowledge and skills. Since there are many different solutions, students can choose their favorite ways toward the answer(s) and create their unique solution(s). Activities can be the opportunities to make comprehensive use of their mathematical knowledge and skills. Every student can respond to the problem in some significant ways of his / her own. There are various kinds of students in a mathematics classroom. Therefore, it is very important for every student to be involved into the classroom activities, and the lessons should be pitched at a level of understanding suitable for every student. Open-ended problems provide every student with the opportunities to find his / her own answer(s). The lesson can encourage students to think critically. Through the comparisons and discussions in the classroom, students are intrinsically motivated to give reasons for their solutions to other students. It is a great opportunity for students to develop their mathematical thinking. There are rich experiences for students to have pleasure of discovery and to receive the approval from fellow students. Since every student has their solution based on their unique thinking, every student will be interested to find out more about their fellow students’ solutions. Act it out This strategy is to enable the learners to visualise the contents of the problems and what is involved. They go through the actions of what the problem says and to come to a conclusion. The physical action makes the problem components and their relationship clearer in the students’ minds. When teaching this strategy, it is important to stress that alternative objects can be used instead of using the actual real things. Children are very good at pretending so they will probably suggest substituting objects anyway. Teachers need to make sure the attention is on the actions and not the actual objects. An easy problem to solve is, 'Six children are standing at the teacher's desk. Four more join them. How many are at the teacher's desk now?' The value of acting out the problem is that it will make the problem becomes clearer. If the problem is hard, then it may be more important to act it out and show relationships. Act it out is one of the important strategies in Heuristic Math. It makes students form mathematical concepts which are well established. It encourages them to be inventive, aids concept and skill development and boost the understanding of the process. Students will be able to visualise the problems clearly. Students using this method will develop innovation, confidence, creativity and independence. It is a great strategy for students who have difficulties with understanding complex problems and a great tool to simplify the process of finding solutions. Many young kids enjoy using this strategy as they can role-play the problem. It is very effective if applied in a small group. The negative side is that it can be cumbersome when used in larger groups. Getting involved in the problems also help students to get focus as they will be engrossed in the mechanics of what they are doing. As a result, they can get more out of it and remember it longer than normal. This strategy may be used as a combination with other strategies like drawing a diagram, using model method, guess and check, etc. The above are introductions to the various heuristics. For examples of how to apply the various Heuristics, do download the sample questions. Have fun solving problems using Heuristics!